PythonでVARモデルからインパルス応答推定をしてみる

↓の記事で書かれているインパルス応答をPythonでやってみるってだけの内容です。

・Rで計量時系列分析：VARモデルから個々の時系列データ間の因果関係を推定する
http://tjo.hatenablog.com/entry/2013/07/30/191853

使うデータは沖本先生のページからMSCIのデータを使います。
ホントはこのブログのPV数とかセッション数で試してみたかったんですが、インパルスになるようなデータが無いんですよねー残念。

やり方は以下です。

%matplotlib inline
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.api import VAR, DynamicVAR
import pandas as pd
import seaborn as sns

# prepare the dates index
df = pd.read_csv("C:\\Users\\msci.csv",skiprows=1, names=['Date','ca','fr','ge','it','jp','uk','us']).dropna()
from statsmodels.tsa.base.datetools import dates_from_str
tmd = pd.to_datetime(df['Date'])
df.index = tmd
del df["Date"]

MSCIのデータを読み込んでデータフレームにしています。

data = pd.DataFrame(index=df.index)
data['jp'] = np.log(df['jp']) - np.log(df['jp'].shift(1))
data['uk'] = np.log(df['uk']) - np.log(df['uk'].shift(1))
data['us'] = np.log(df['us']) - np.log(df['us'].shift(1))

これで日本とイギリスとアメリカの株式収益率を計算しています。
対数差分を取っているわけですね。

# make a VAR model
model = VAR(data[:-1].dropna())
model.select_order(15)
                 VAR Order Selection                  
======================================================
            aic          bic          fpe         hqic
------------------------------------------------------
0        -27.57       -27.56    1.059e-12       -27.57
1        -27.98      -27.94*    7.035e-13       -27.97
2        -28.01       -27.93    6.832e-13      -27.98*
3       -28.01*       -27.90   6.825e-13*       -27.97
4        -28.01       -27.86    6.866e-13       -27.95
5        -28.00       -27.82    6.891e-13       -27.94
6        -28.00       -27.79    6.884e-13       -27.92
7        -28.00       -27.74    6.944e-13       -27.90
8        -27.99       -27.71    6.979e-13       -27.88
9        -27.99       -27.67    7.019e-13       -27.87
10       -27.98       -27.63    7.031e-13       -27.85
11       -27.98       -27.59    7.045e-13       -27.84
12       -27.98       -27.56    7.065e-13       -27.82
13       -27.97       -27.51    7.143e-13       -27.80
14       -27.96       -27.47    7.190e-13       -27.78
15       -27.95       -27.43    7.257e-13       -27.76
======================================================
* Minimum

Out[10]: {'aic': 3, 'bic': 1, 'fpe': 3, 'hqic': 2}

モデルはVAR(3)にします。

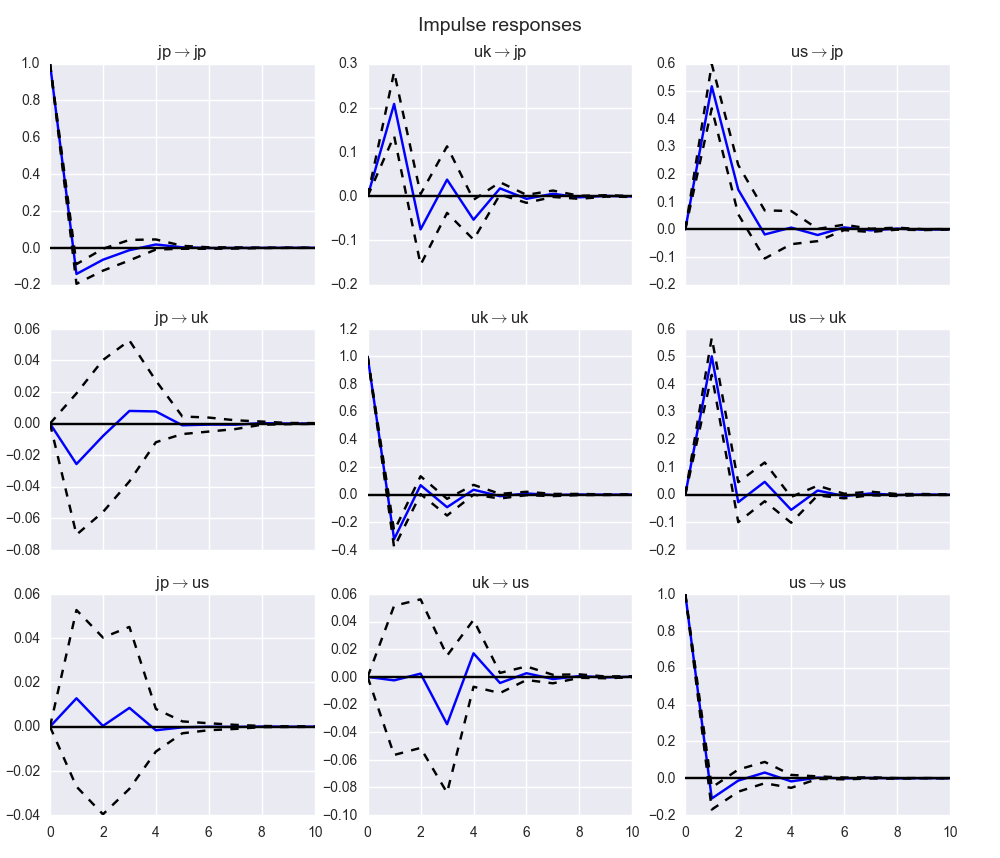
results = model.fit(maxlags=15, ic='aic')

#インパルス応答
irf = results.irf(10)
irf.plot(orth=False)

沖本先生の本と結果がちょっと異なっていましたが、だいたい合っている気がします！多分！
このグラフから以下のことがわかります。

■日本市場における1標準偏差のショック
日本市場における1標準偏差のショックは1%程度のショックであるが、同日の影響はほぼなし。日本市場において、株価が1%程度上昇もしくは下落したとしても、それが他国の株式市場に与える影響は限定的。

■イギリス市場における1標準偏差のショック
日本市場に対しては1日後に正で大きな持ち、アメリカ市場に対しては同日に正で大きな影響を持つ。具体的にはイギリス市場において、予想外に株価が0.1%程度上昇するようなことがあったとすると、次の日の日本市場の株価は期待されていた水準よりも0.21%程度上昇する。同日のアメリカ市場へはほぼ影響がない。

■アメリカ市場における1標準偏差のショック
1日後のイギリス市場に対して正で大きな影響をもつが、2日目以降は大きな影響はもたない。また、日本市場に対しては1日後に正で大きな影響を持ち、2日後もわずかながら正の影響をもつ。アメリカ市場に負のショックがあったとすると、アメリカ市場における1%程度の株価の下落は、1日後に日本の株価を0.5%程度下落させ、2日後にさらに0.12%程度下落させる。また、同様の下落は1日後のイギリスの株価を0.5%程度下落させる。

なるほどーという感じです。
何かに使えそうな予感がしますね。

[参考]
PythonでVarモデルで推定する場合のサンプルです。
・Vector Autoregressions tsa.vector_ar
http://statsmodels.sourceforge.net/devel/vector_ar.html

標準偏差とはなんぞや？については以下に詳しく書かれています。
・【統計学】初めての「標準偏差」（統計学に挫折しないために）
http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619

VARモデルについての説明は以下が分かりやすかったです。
・VARモデル
http://logics-of-blue.com/var%E3%83%A2%E3%83%87%E3%83%AB/

PythonでVARモデルからインパルス応答推定をしてみる

関連する投稿:

投稿者: kaz

コメントを残すコメントをキャンセル

関連する投稿:

投稿者: kaz

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル