季節調整済みARIMAモデルで電力使用状況を推定してみる
北海道電力の電力使用状況を季節調整済みARIMAモデル(Seasonal ARIMA)で推定してみました。そのメモです。
このサイトを参考にしました。ほぼそのままやりました。
■Seasonal ARIMA with Python
http://www.seanabu.com/2016/03/22/time-series-seasonal-ARIMA-model-in-python/
このブログでも紹介されていますが、statsmodelsのdevelopment versionが必要です。
https://github.com/statsmodels/statsmodels
これをインストールするにはvisual c++のなんかのバージョンが必要で色々と面倒でした。あと、pipでインストールすると失敗するのでeasy_installでうまくいく場合もありました。
%pylab
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta
import seaborn as sns #グラフが見やすくなる
import statsmodels.api as sm
from statsmodels.tsa.stattools import acf
from statsmodels.tsa.stattools import pacf
from statsmodels.tsa.seasonal import seasonal_decompose
data = pd.read_csv("http://denkiyoho.hepco.co.jp/data/2016_juyo_hokkaidou.csv", skiprows=3,names=['Date','Time','power'])
data.index = pd.to_datetime(data['Date'])
df = data.groupby(data.index).mean()
df['power'] = df.power.apply(lambda x: int(x)*10000)
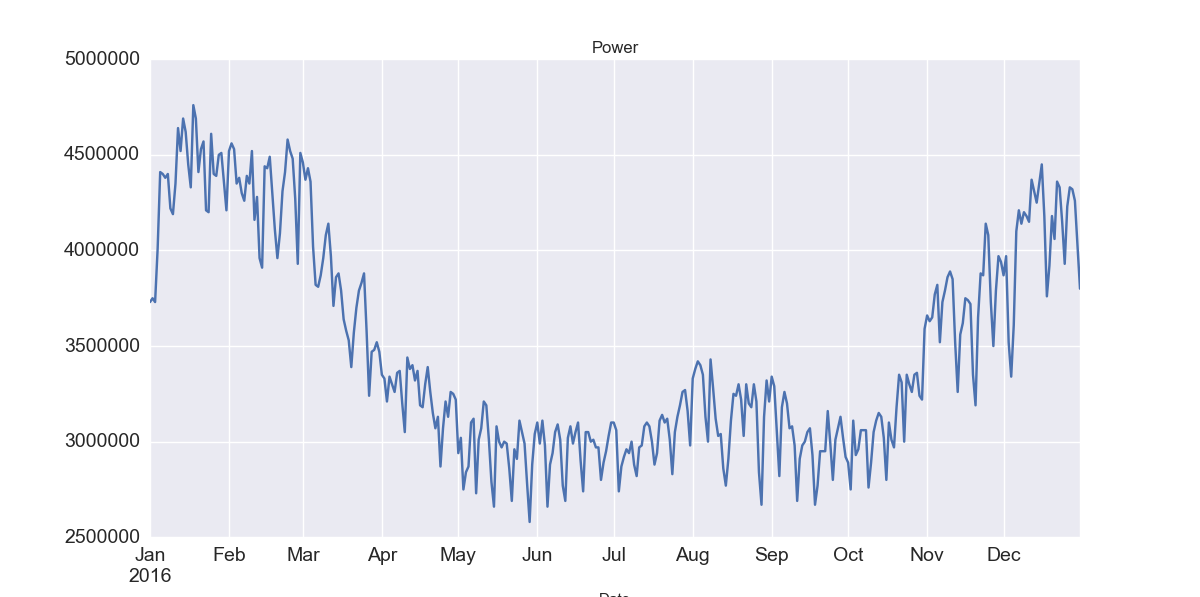
df.power.plot(figsize=(12,6), title= 'Power', fontsize=14)
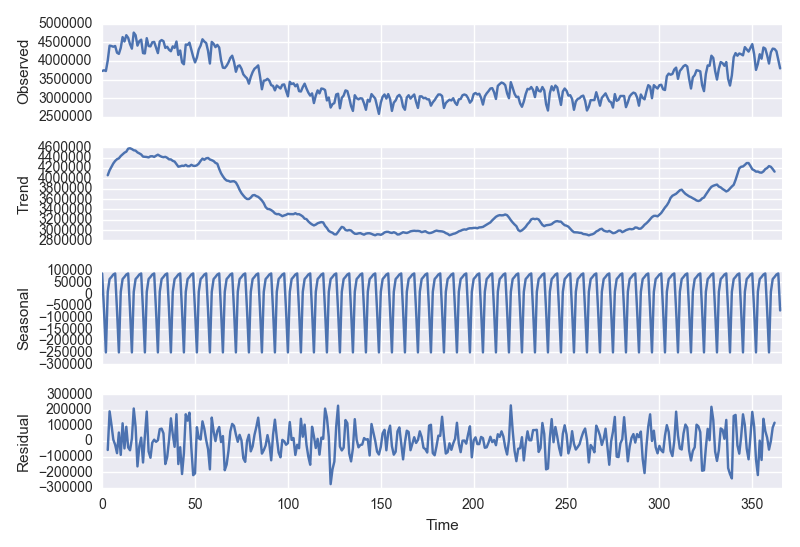
ここからトレンド、季節変動、、残差(ランダム成分)にわけます。
plt.close() df = pd.DataFrame(df['power'].values.astype(int), pd.DatetimeIndex(start='2016-01-01', periods=len(df['power']), freq='D')) df.columns= ['power'] decomposition = seasonal_decompose(df.values, freq=7) fig = plt.figure() fig = decomposition.plot() fig.set_size_inches(8, 8)
ここから定常性を確認します。参考にした記事に良いものがありましたので使わせてもらいます。
plt.close()
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = pd.rolling_mean(timeseries, window=7)
rolstd = pd.rolling_std(timeseries, window=7)
#Plot rolling statistics:
fig = plt.figure(figsize=(8, 6))
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show()
#Perform Dickey-Fuller test:
print ("Results of Dickey-Fuller Test:")
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print (dfoutput)
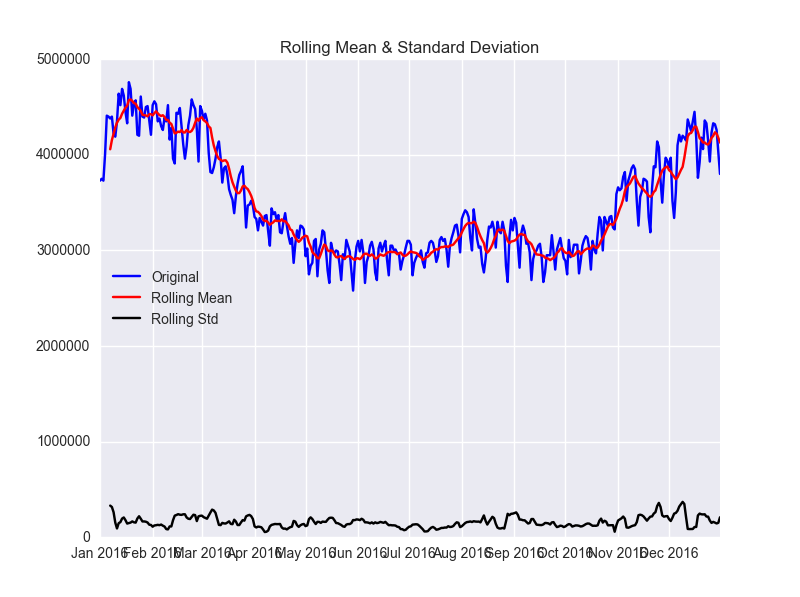
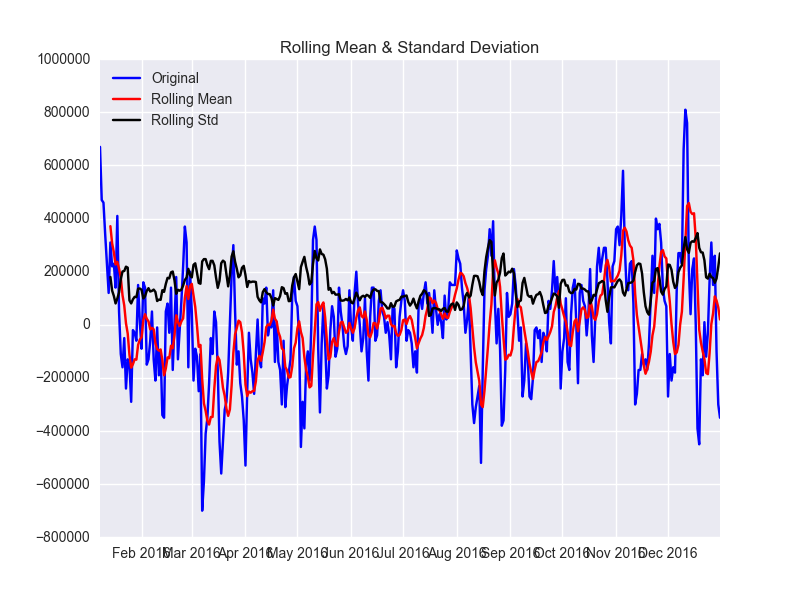
test_stationarity(df.power)
###Results of Dickey-Fuller Test:###
Test Statistic -1.832150
p-value 0.364621
#Lags Used 14.000000
Number of Observations Used 351.000000
Critical Value (1%) -3.449119
Critical Value (5%) -2.869810
Critical Value (10%) -2.571176
dtype: float64
データは定常性ではないことがわかります。
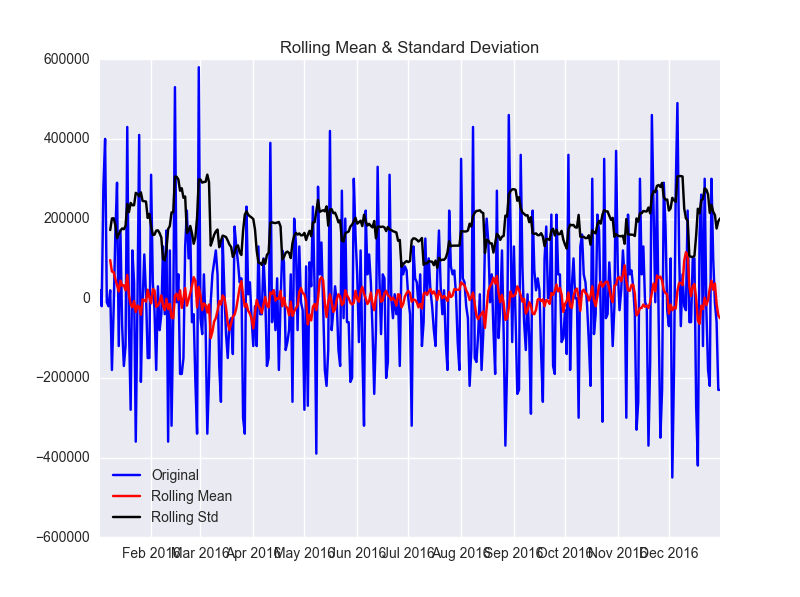
次に1次の差分をとった場合です。
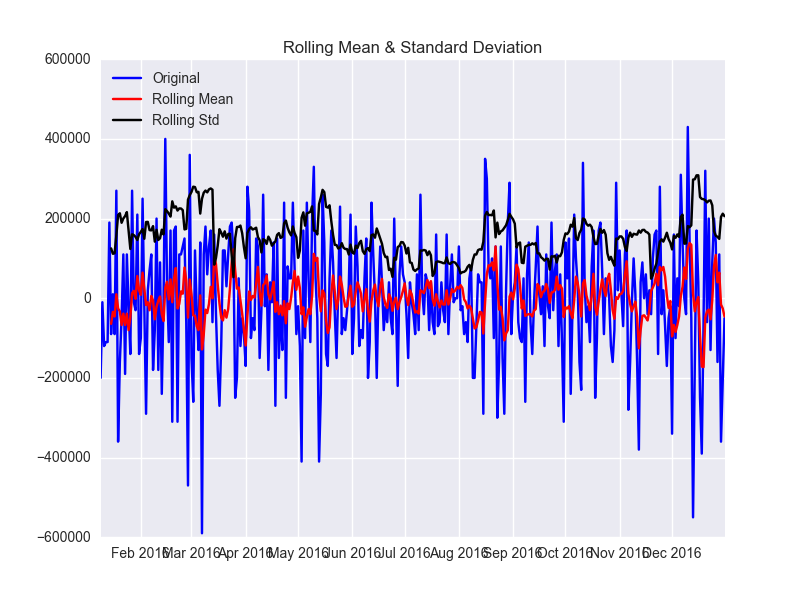
plt.close() df['first_difference'] = df.power - df.power.shift(1) test_stationarity(df.first_difference.dropna(inplace=False)) ###Results of Dickey-Fuller Test:### Test Statistic -5.660888e+00 p-value 9.385886e-07 #Lags Used 1.300000e+01 Number of Observations Used 3.510000e+02 Critical Value (1%) -3.449119e+00 Critical Value (5%) -2.869810e+00 Critical Value (10%) -2.571176e+00 dtype: float64
次は季節性の差分をとります。
plt.close() df['seasonal_difference'] = df.power - df.power.shift(7) test_stationarity(df.seasonal_difference.dropna(inplace=False)) ###Results of Dickey-Fuller Test:### Test Statistic -3.452940 p-value 0.009281 #Lags Used 14.000000 Number of Observations Used 344.000000 Critical Value (1%) -3.449503 Critical Value (5%) -2.869979 Critical Value (10%) -2.571266 dtype: float64
一次の差分と、季節性を取り除きます。
plt.close() df['seasonal_first_difference'] = df.first_difference - df.first_difference.shift(7) test_stationarity(df.seasonal_first_difference.dropna(inplace=False)) ###Results of Dickey-Fuller Test:### Test Statistic -9.147004e+00 p-value 2.750689e-15 #Lags Used 1.300000e+01 Number of Observations Used 3.440000e+02 Critical Value (1%) -3.449503e+00 Critical Value (5%) -2.869979e+00 Critical Value (10%) -2.571266e+00 dtype: float64
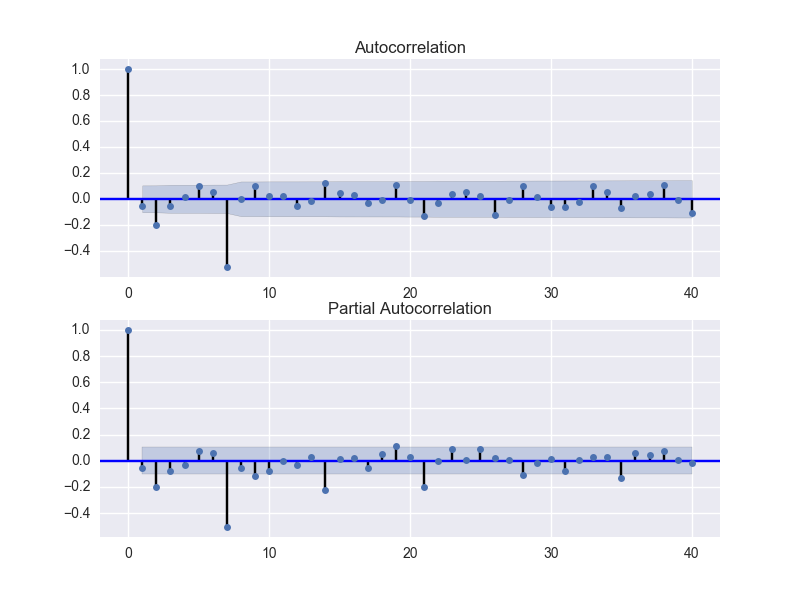
ACFとPACFからパラメータを選びます。
plt.close() fig = plt.figure(figsize=(8,6)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(df.seasonal_first_difference.iloc[8:], lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(df.seasonal_first_difference.iloc[8:], lags=40, ax=ax2)
こちらを参考にモデルのパラメータを選べばいいそうです。
■ARIMA models for time series forecasting
http://people.duke.edu/~rnau/arimrule.htm
もっと簡単にパラメータを選ぶ方法があればいいと思いますが、ないんですかね?
seasonal_order=(0,1,1,7)とseasonal_order=(1,1,1,7)でモデルを作成してみました。
plt.close()
mod = sm.tsa.statespace.SARIMAX(df.power, trend='n', order=(0,1,0), seasonal_order=(0,1,1,7))
results = mod.fit()
print (results.summary())
Statespace Model Results
=========================================================================================
Dep. Variable: power No. Observations: 366
Model: SARIMAX(0, 1, 0)x(0, 1, 1, 7) Log Likelihood -4772.423
Date: Thu, 09 Mar 2017 AIC 9548.846
Time: 21:04:58 BIC 9556.607
Sample: 01-01-2016 HQIC 9551.932
- 12-31-2016
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ma.S.L7 -0.4498 0.012 -36.021 0.000 -0.474 -0.425
sigma2 1.674e+10 2.7e-13 6.21e+22 0.000 1.67e+10 1.67e+10
===================================================================================
Ljung-Box (Q): 50.61 Jarque-Bera (JB): 1021.36
Prob(Q): 0.12 Prob(JB): 0.00
Heteroskedasticity (H): 0.52 Skew: -1.32
Prob(H) (two-sided): 0.00 Kurtosis: 10.84
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 1.36e+37. Standard errors may be unstable.
mod = sm.tsa.statespace.SARIMAX(df.power, trend='n', order=(0,1,0), seasonal_order=(1,1,1,7))
results = mod.fit()
print (results.summary())
Statespace Model Results
=========================================================================================
Dep. Variable: power No. Observations: 366
Model: SARIMAX(0, 1, 0)x(1, 1, 1, 7) Log Likelihood -4745.075
Date: Thu, 09 Mar 2017 AIC 9496.150
Time: 21:06:44 BIC 9507.792
Sample: 01-01-2016 HQIC 9500.780
- 12-31-2016
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.S.L7 0.4606 0.020 22.704 0.000 0.421 0.500
ma.S.L7 -0.9589 0.030 -32.239 0.000 -1.017 -0.901
sigma2 1.614e+10 2.89e-13 5.57e+22 0.000 1.61e+10 1.61e+10
===================================================================================
Ljung-Box (Q): 88.63 Jarque-Bera (JB): 7.99
Prob(Q): 0.00 Prob(JB): 0.02
Heteroskedasticity (H): 0.63 Skew: -0.26
Prob(H) (two-sided): 0.01 Kurtosis: 3.52
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number inf. Standard errors may be unstable.
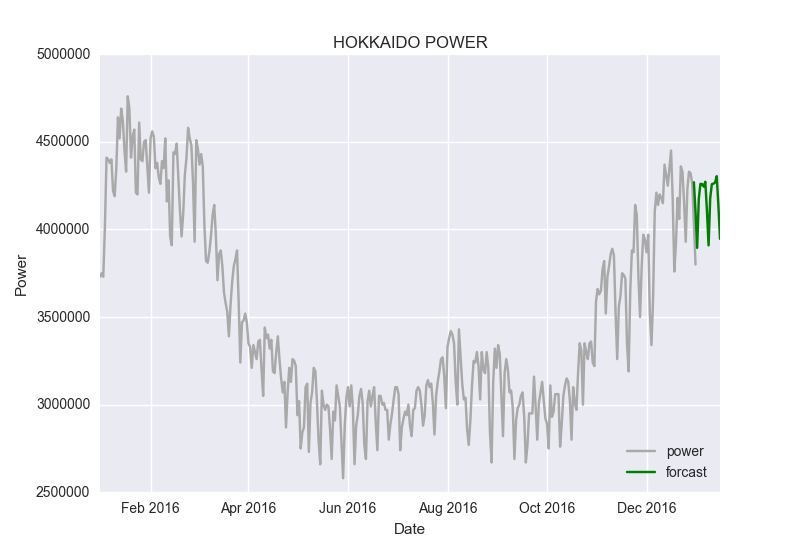
seasonal_order=(1,1,1,7)のほうがAICとBICの値が小さくなっていましたのでseasonal_order=(1,1,1,7)でグラフにしてみます。
fig, ax = plt.subplots()
ax.set(title='HOKKAIDO POWER', xlabel='Date', ylabel='Power')
ax.plot(df.power.ix['2016-01-01':], 'g',label="power",color="darkgrey")
ax.plot(results.predict(start = 364, end= 380, dynamic= True),'g',label="forcast",color="green")
legend = ax.legend(loc='lower right')
legend.get_frame().set_facecolor('w')
ほほーという感じですね。もう少しいろいろなデータで検証してみたいと思います。
※参考
■Statsmodels Examples
http://www.statsmodels.org/devel/examples/index.html
■Rで季節変動のある時系列データを扱ってみる
http://tjo.hatenablog.com/entry/2013/10/30/190552
関連する投稿:
- 2017-02-11:Python3でビットコインの回帰線を描いてみる
- 2017-03-14:季節調整済みARIMAモデルで電力使用状況を推定してみる part2 予測表示
- 2017-01-25:軍需企業の株価
- 2017-03-17:SARIMAXモデルでPVを予測してみる
- 2017-02-24:電力データから季節変動の分解
“季節調整済みARIMAモデルで電力使用状況を推定してみる” への2件の返信