Python3でビットコインの回帰線を描いてみる
現在のビットコインの値段の推移はどうなっているのか調べてみました。
%matplotlib inline
import datetime as dt
import pandas as pd
import matplotlib.pyplot as plt
btc = pd.read_csv("https://api.blockchain.info/charts/market-price?format=csv", names=['Date', 'Value'])
tmd = pd.to_datetime(btc['Date'])
btc.index = tmd
btc.plot(color='darkblue')
plt.ylabel('BITCOIN')
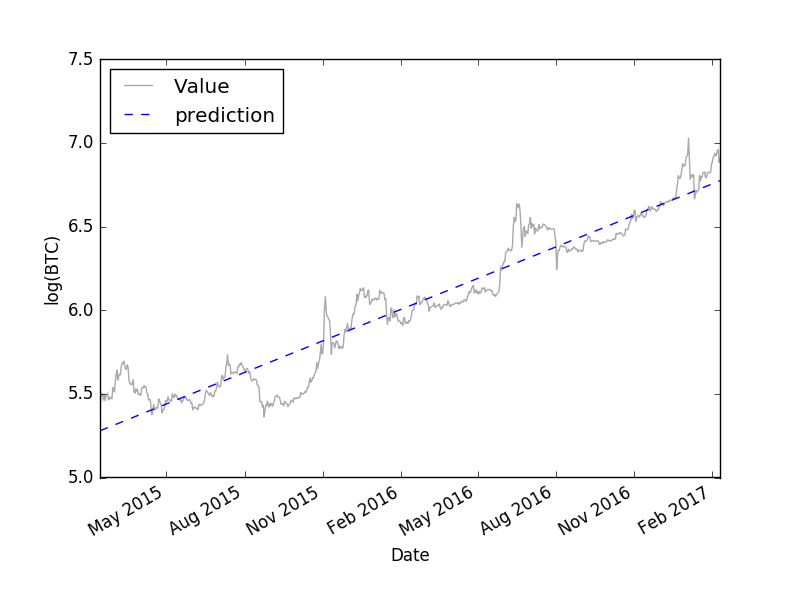
ついでにビットコインの対数の回帰線も調べてみます。
import statsmodels.api as sm
import numpy as np
lnnbtc=np.log(btc['Value'].dropna())
y=lnnbtc
x=range(len(lnnbtc)) #lnnbtcと同じ長さに設定
x=sm.add_constant(x) #線形回帰の切片のために列(要素)を作成
model=sm.OLS(y,x) #線形回帰分析を設定modelとして保存
results=model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Value R-squared: 0.914
Model: OLS Adj. R-squared: 0.914
Method: Least Squares F-statistic: 7707.
Date: Sat, 11 Feb 2017 Prob (F-statistic): 0.00
Time: 20:26:09 Log-Likelihood: 438.28
No. Observations: 730 AIC: -872.6
Df Residuals: 728 BIC: -863.4
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const 5.2796 0.010 537.106 0.000 5.260 5.299
x1 0.0020 2.33e-05 87.790 0.000 0.002 0.002
==============================================================================
Omnibus: 2.417 Durbin-Watson: 0.045
Prob(Omnibus): 0.299 Jarque-Bera (JB): 2.273
Skew: 0.131 Prob(JB): 0.321
Kurtosis: 3.076 Cond. No. 841.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R-squared(決定係数):0.914となっているのでイイ感じなんじゃないでしょうか。
plt.plot(y,label='Value',color="darkgray")
results.fittedvalues.plot(label='prediction',style='--')
plt.ylabel('log(BTC)')
plt.legend(loc='upper left')
関連する投稿:
- 2017-01-25:軍需企業の株価
- 2017-03-09:季節調整済みARIMAモデルで電力使用状況を推定してみる
- 2021-05-16:気になるETFのメモ
- 2017-02-24:電力データから季節変動の分解
- 2017-03-14:季節調整済みARIMAモデルで電力使用状況を推定してみる part2 予測表示